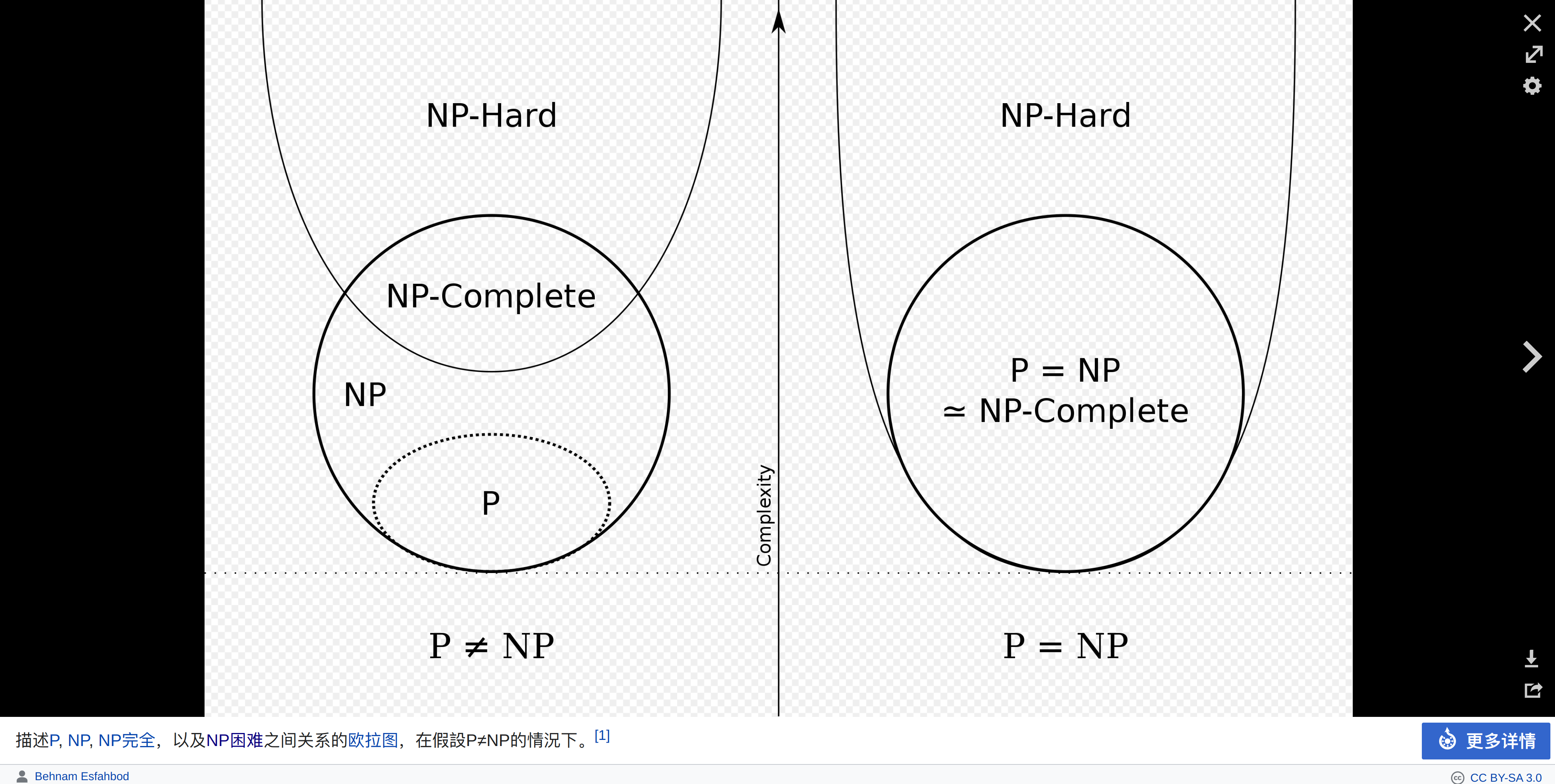
(2023年6月)Introduction to Linear Optimization学习笔记1
臃肿的笔记,学习范畴大概是从“不知道线性规划是什么“到”勉强理解了simplex algorithm的作用和一些细节”,但不涉及simplex题目(比如Tableau的计算)。因为错过了纠正本篇笔记的最佳时机(2023年12月),现在(2024年8月)已经忘光了LP的大部分内容,所以本篇笔记的错误内容也不知道什么时候能纠正了,只能先把笔记发出来。
目录:
2024年写的总结
关于这篇笔记
最简单的线性规划例题(高考)
准备一些资料
本篇笔记主要参考的
原始笔记
bilibili猴博士-运筹学视频
介绍
p1 线性规划建模
p3 图解法
p2 化标准型
p4 单纯形法
(2023年9月补充)标准型和规范型(standard form/canonical form)
过渡内容:尝试系统学习一下单纯形法
博客:Visualizing the Simplex Algorithm – Daniel Nichols
part1
对解空间的理解
降低计算量:解空间的顶点
进一步减少计算量:顶点游走
过渡到下一篇要看的博客
复习一些矩阵概念
线性无关
高斯消元法
增广矩阵
秩
临时记的几个小问题
对秩的一些混乱理解笔记
转置,秩,维度变化
秩与解空间的维度关系
博客:简单理解线性规划的单纯形算法(zhihu.com)
part1
基解,可行解,基可行解
出基和入基
理解笔记
中途思考的问题
出基和入基(2)
遇到了理解不了的内容,准备换资料看
参考书《最优化理论与算法》P37~P40
完整PDF存档
帮助理解的最关键一步:对x_k的理解
对x_k的其他限制
迭代最后一步:交换(遗留一个小问题)
单纯形法的终止条件
simplex algorithm完整步骤
遗留的3个问题(解决了2/3)
几天以后,对参考书《最优化理论与算法》P37~P40的重新理解
为什么会有这部分笔记
矩阵与向量的变化
一些手写笔记
从min()切换到max()