（导航）（2023年6月~7月）基于MIT 6.251J Introduction to Mathematical Programming学习LP（只学到simplex前后）

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

课程网页：🔗 [Syllabus | Introduction to Mathematical Programming | Electrical Engineering and Computer Science | MIT OpenCourseWare] https://ocw.mit.edu/courses/6-251j-introduction-to-mathematical-programming-fall-2009/pages/syllabus/

大纲：

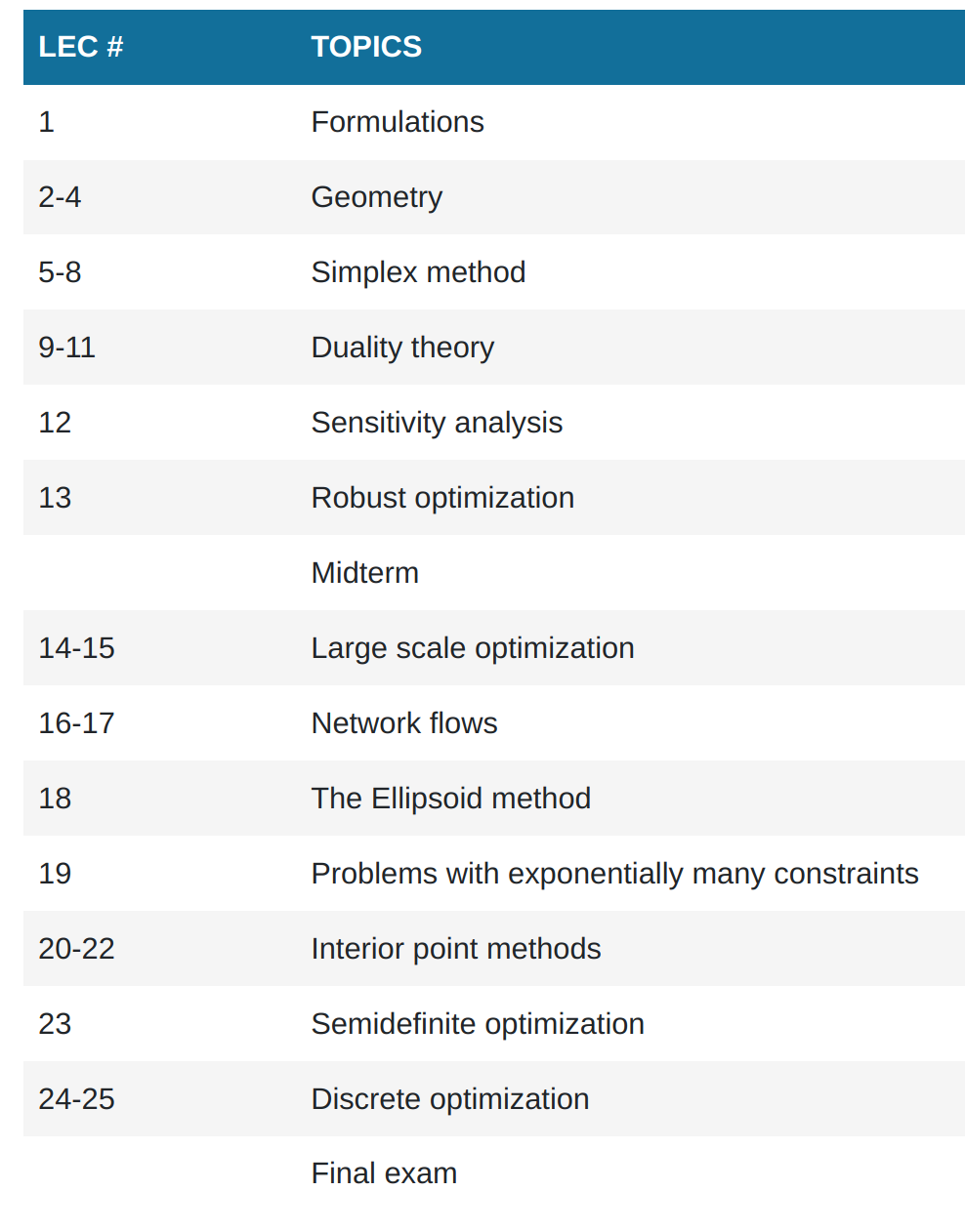
配套的是introduction to linear optimization这本书：

2023年6月之前：对下面的这些知识完全一无所知：

1. 线性规划/线性优化/linear programming/LP
2. 广义上的优化问题
3. 优化问题对应的空间问题（Geometry；也就是说，线性代数的知识忘光了）
4. 其他线性代数的知识，包括矩阵计算、矩阵公式的推导

所以从2024年的角度来看，直接用MIT intro to linear optimization这本书（或者说MIT 6.251J这门课）开始学习，并强行试图去做书上的一些习题，是不太合理的。我在degeneracy这块地方卡了很久，最终这个系列也就学到simplex就停了。

学习的过程基本上就是：

1. 基本没有跟着MIT这门课的slides或者这本书的讲述顺序学习，而是到处狂找各种更简单入门的资料先去看
2. 中途狂补各种线性代数的知识（多胞体，仿射，秩这些）
3. 发现进入了知识嵌套（知识A依赖于知识B，知识B依赖于知识C，知识C依赖于知识D），学了一个下午都有可能做不出最开始的那道题
4. 卡在simplex和degeneracy这两个话题上
5. 最后强行收尾不学了，也就是学到simplex和degeneracy这块

更合适的学习顺序应该是从LP and network flowing这本书的【practical exercise】开始入手（就是带有实际数字的各种以tableau为核心的题），好处有：

1. 因为题目简单，网上的解答也多
2. 实践题能用求解器验证答案是否正确（MIT这本书的抽象题就算做了也不敢说自己证明得对不对）
3. 能快速从“列LP算式“学到”dual theory“，差不多就走完了入门linear programming的一个流程。学完dual theory以后回头能看懂之前疑惑的很多问题
4. 学得快，不容易有挫败感
5. 就算没有彻底弄懂一些理论内容（比如duality/lagrange在空间层面的理解），也能学会一些实践内容，很多场合下完全够用了