This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.原始标题：基于无向图模型的simulator（无框架, python, agent-based）
实际上本篇笔记大部分内容都是dijkstra而且没有完全学明白
无向图模型，G = <V, E>，图模型来自于对shapefile（.shp）文件的读取
然后运行Dijkstra Algorithm，可能会使用改良过的算法
需要考虑agent的位置处于Edge中间的状态（从一个Vertex到达另一个Vertex需要时间），但目前不会对Dijkstra算法或agent的运动产生影响
🔗 [GeospatialPython/pyshp: This library reads and writes ESRI Shapefiles in pure Python.] https://github.com/GeospatialPython/pyshp#reading-shapefiles
Dijkstra算法
翻了一圈，发现整个博客都没写过这个算法的笔记
🔗 [戴克斯特拉算法 - 维基百科，自由的百科全书] https://zh.wikipedia.org/zh-hans/戴克斯特拉算法
几个关键点：
伪代码：
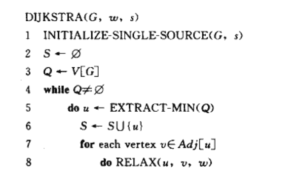
思考1：算法为什么第一眼看起来不严谨，但实际上是严谨的
以这张图为例，D点为出发点：
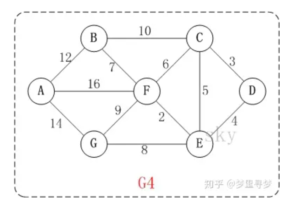
按照算法，把E从集合Q拿出来放到集合S的时候，d[E]=4，且这个数值放到集合S以后就不会再变了。但事实上我们做到这一步的时候只接触了D、C、E、F这几个点，连E <--> G这条边都没摸过，为什么就敢直接把E永久移动到集合S并且再也不用改变它的数值？
或者说，按照上面的疑问，如果故意做出这样一张图，还是从D点出发，Dijkstra算法会如何解决这个看起来故意针对上述疑惑的图？（也就是说，会不会存在一种情况，看似找到了通往E的最短距离DE = 4，但实际上还藏着一条很深很绕很长的路DKLME，这条路实际上拥有最短距离2）
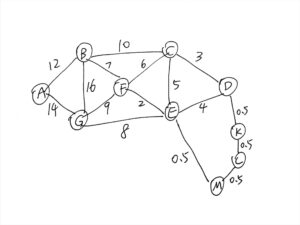
所以Dijkstra算法的另一个重点是“从集合Q中弹出拥有最小数值的节点”（所以集合Q一般采用priority queue来实现）
如果用纸笔去推上面这张图的时候就会发现，由于每次都要弹出最小数值的节点，所以前几步一直都在弹出K, L, M...直到这些步骤都完成后才把d[E]=2从集合Q中弹出来加入集合S.
所以另一个直观的看法就是，Dijkstra算法类似于从出发地点 灌水渗透/放一大堆蚂蚁，或者说，想象一下广度优先搜索的样子
邻接矩阵和邻接表
这两种数据结构的实现都忘记了，反正google搜Dijkstra算法永远能看到各大博客在对比这两种实现方式
看到有些网页说这两种存储方式仅仅是影响图模型的构建，还有的网页说这两种存储方式不仅影响图模型还影响Dijkstra算法本身
等待后续补充结论
现在学会的Dijkstra算法只能做这件事：已知出发点D和目标点E，求D到E的最短路径距离
还没有学会：如何在Dijkstra算法的步骤中保存（或像DP那样回溯）最短路径，如何重复利用最短路径的数据（涉及到很多agents同时搜索，是不是每个agent寻路的时候都要触发一次完整的Dijkstra算法）
不过好像上面写的“重复利用最短路径的数据“可能用不上太多，因为simulator的graph是动态的，道路的权重（拥堵）会随时变化，所以事先计算的东西起不了作用
现在只需要考虑“如何在Dijkstra算法的步骤中保存最短路径”这个问题即可
