This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.奇怪的线性代数空间思考问题，主要内容是思考Ax≤b形成的空间
🔗 [線性代數基本定理 (一) | 線代啟示錄] https://ccjou.wordpress.com/2009/03/23/線性代數基本定理-一/
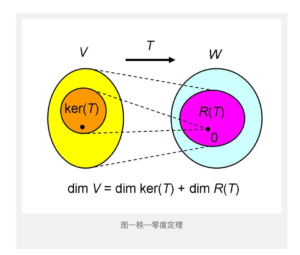
以此理解线性规划方程Ax=b的一些特性（退化解，以及为什么一般默认m x n的矩阵A：m<n）
Ax=b, 假设b是一个10维向量，但Ax=b我们有的时候会画成一个二维平面上的多胞体鸡蛋图形。这个鸡蛋是高维b的投影吗？想象一下b从2维开始增加，投影的变化。
2025-08-15：可能当初写草稿的时候有点偏差，对“多胞体鸡蛋”而言：
整个鸡蛋（包括内部）是Ax<=b的解空间。
鸡蛋的所有表面是在满足Ax<=b的前提下，至少有一个等式成立的点的集合
鸡蛋的一个顶点/一条边/一个面是Ax=b的解空间
这里的“一个面”可能会引发高维度空间对于“面”的定义，所以重新阐述为：对于一个n维的Ax=b（不考虑A=0）如果有解，解空间可以是从(n-1)维到0维（vertex）的任何东西. 如果只有1个解，那么就是vertex，如果有无穷多的解，那么有可能是一条边或者一个二维平面或者一个三维“表面”或者（更高维度空间下的高维度表示方法，直到(n-1)维）.
无论是鸡蛋表面还是整个鸡蛋，在二维平面上的图形都是x的投影（而不是b的投影）.
如果抛开高维空间，只讨论这张图（假设这张图就是3维空间下的Ax<=b形成的空间）：
快速过一遍：
n=3，m很大，这是一个n=3维空间
x：3 x 1的vector
A：m x 3的矩阵
b：m x 1的vector
b是一个行数很多，列数只有1的矩阵
这个多胞体的多个“切削面”来自很多很多[mathjax]A_{i1}x_1+A_{i2}x_2+A_{i3}x_3=b_i[/mathjax]形成的很多很多半空间的“切削”.
[mathjax]A_{i1}x_1+A_{i2}x_2+A_{i3}x_3=b_i[/mathjax]代表什么？代表一个平面
[mathjax]A_{i1}x_1+A_{i2}x_2+A_{i3}x_3\leq b_i[/mathjax]代表什么？代表一个平面形成的半空间。
在满足Ax<=b的前提下，正好有1个等式成立：Ax<=b的解会落在这个多胞体的“表面（二维平面）”上（但不能是vertex/edge）；为什么会落在二维平面的表面上 -> [mathjax]A_{i1}x_1+A_{i2}x_2+A_{i3}x_3=b_i[/mathjax]代表什么？代表一个平面
正好有2个等式成立：Ax<=b的解会落在这个多胞体的edge上（但不能是vertex）；（2个独立的平面确定一条边）
有3个等式成立：Ax<=b的解会落在这个多胞体的vertex上（也就是图中的橘黄色点）；（3个独立的平面确定一个点）
但m很大，如果有4个等式成立，Ax<=b的解会落在哪里呢？上一步已经到了vertex，似乎不能再“进一步”了！
答案是，如果有4个等式成立，Ax<=b的解会落在这个多胞体的degeneracy vertex上面。依然是vertex，只是这个顶点是退化解。（4个独立的平面确定一个点）
