This post was published in 2023-07-19. Obviously, expired content is less useful to users if it has already pasted its expiration date.
Table of Contents
前置
这篇笔记写在A1和A2做完以后(A2留了2道题没做)
一系列可能有关联的概念:
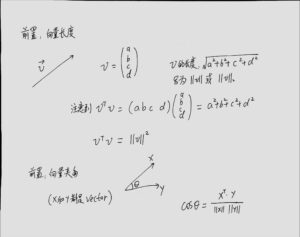
特征值,特征向量,内积,投影,正定,[mathjax]\cos(\theta)[/mathjax](向量之间的夹角)
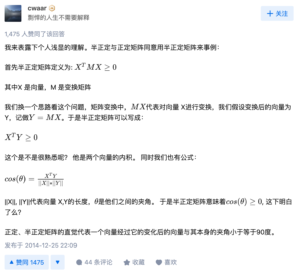
正定 positive-definite
正定 positive-definite:
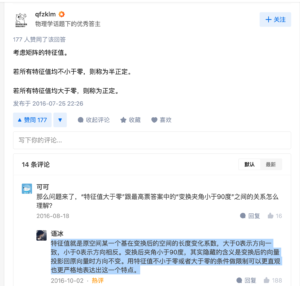
🔗 [请问谁能用易于理解的语言解释下矩阵的正定及半正定? - 知乎] https://www.zhihu.com/question/22098422
特征值与特征向量
特征值与特征向量
参考过资料:
🔗 [如何理解矩阵特征值? - 知乎] https://www.zhihu.com/question/21874816
🔗 [【熟肉】线性代数的本质 - 10 - 特征向量与特征值_哔哩哔哩_bilibili] https://www.bilibili.com/video/BV1Ls411b7oL/
总结:正定/半正定/特征值/特征向量
总结上面的内容:正定/半正定/特征值/特征向量
正定矩阵 positive-definite matrix
半正定矩阵 positive semi-definite matrix
半负定矩阵 negative semi-definite matrix
负定矩阵 negative-definite matrix
不定矩阵 indefinite matrix
特征值和 Eigenvalues
特征向量 eigenvectors
接下来涉及的矩阵乘法都是这个样子的:
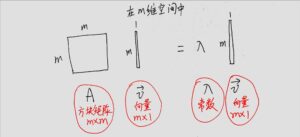
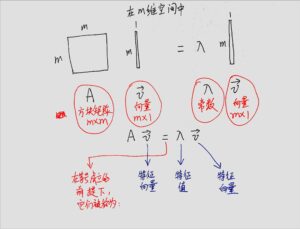
上面这张图的等式要想成立其实并不容易,如果方块矩阵[mathjax]A[/mathjax]是固定不动的,只有少部分向量[mathjax]\overrightarrow{v}[/mathjax]才能满足等式成立。
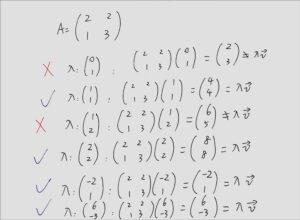
等式成立的时候就像这样:
所以,这个完整的过程大概是:
下面的内容主要来自对3blue1brown视频(BV1Ls411b7oL)的总结
方块矩阵[mathjax]A[/mathjax]:代表着对当前[mathjax]m[/mathjax]维空间的一种“坐标变换”(把空间扭曲成其他样子)
也就是说,上述等式的左半部分[mathjax]A\overrightarrow{v}[/mathjax]的意思就是说:对当前空间施加固定的空间变换规则[mathjax]A[/mathjax],这样原空间的每个向量[mathjax]\overrightarrow{v}[/mathjax]在新的空间都变成了另一个向量(维度都是m x 1,只是数字变了)。
但仍然有少部分向量[mathjax]\overrightarrow{v}[/mathjax]在空间扭曲以后的方向不变,只是在同一个方向上拉伸了(有正方向拉伸,负方向拉伸,或者缩成0),这些特殊的向量就是 特征向量 [mathjax]\overrightarrow{v}[/mathjax];空间扭曲变换后拉伸的系数就是 特征值 [mathjax]\lambda[/mathjax].
求解过程大概是这样的:
最关键的一步其实是用[mathjax]\text{I}\lambda[/mathjax]代替[mathjax]\lambda[/mathjax]:
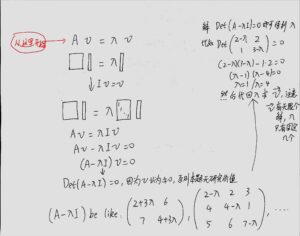
例题:(来自3Blue1Brown的视频BV1Ls411b7oL)
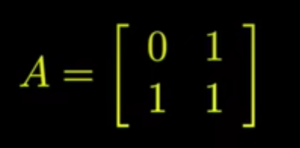
2个特征向量举例为
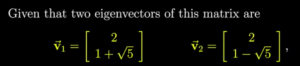
特征值和特征向量差不多会算了,接下来回到最开始的正定矩阵的定义
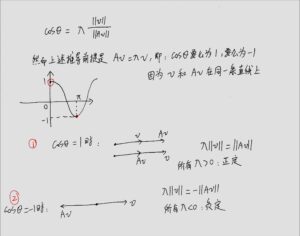
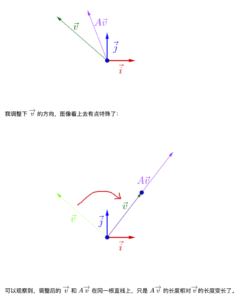
尝试用公式推导理解这两张图(尤其是对余弦相似度[mathjax]\cos(\theta)[/mathjax]的理解):


理解为: