2021-11-10

WARNING: This article may be obsolete
This post was published in 2021-11-10. Obviously, expired content is less useful to users if it has already pasted its expiration date.

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

字符串匹配算法：brute force, KMP, Boyer-Moore

⚫️ 让brute force达到worst case的匹配情形举例：

AAABAAABAAABAAABAAAB

AAAA

⚫️ 如果匹配的机制是“找出所有匹配情形”，而不是“返回第一个匹配情形”，那么让Boyer-Moore达到worst case的匹配情形举例：

AAAAAAAAAAAAAAAAAAAAAAAAA

AAAAAA

⚫️ 对于Boyer-Moore算法，详细的time complexity分析会变得十分复杂，见：🔗 [分享一下字符串匹配BM算法学习心得。 - 南柯一喵 - 博客园] https://www.cnblogs.com/a180285/archive/2011/12/15/BM_algorithm.html

⚫️ KMP算法的优缺点：

Leetcode 1143: Longest Common Subsequence （LCS）

快速复习策略：

原题，用来验证自己是否做对：🔗 [Longest Common Subsequence - LeetCode] https://leetcode.com/problems/longest-common-subsequence/

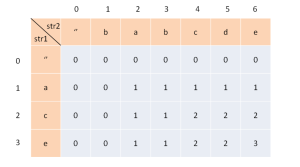
从空表开始，手动填写这个DP table：

填写顺序：逐行填写（每一行都从左往右填写），填完一行再填一行

DP状态方程的构造问题：

核对答案：（答案来自https://leetcode-cn.com/problems/longest-common-subsequence/solution/dong-tai-gui-hua-zhi-zui-chang-gong-gong-zi-xu-lie/，但无需看来源的解析）

最后去leetcode原题上面跑结果进行验证。