2021-11-02

WARNING: This article may be obsolete
This post was published in 2021-11-02. Obviously, expired content is less useful to users if it has already pasted its expiration date.

This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.

KMP算法

🔗 [字符串匹配的Boyer-Moore算法 - 阮一峰的网络日志] https://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html

Boyer-Moore算法

🔗 [字符串匹配的Boyer-Moore算法 - 阮一峰的网络日志] https://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html

🔗 [字符串匹配 - Boyer–Moore 算法原理和实现 | 春水煎茶 - 王超的个人博客] https://writings.sh/post/algorithm-string-searching-boyer-moore

两种常见的Numpy数组

这部分内容是在2022-09-25补充的：

首先认识一下最常见的2种类型的numpy array（下面2张图分别生成了 a 和 b ）：

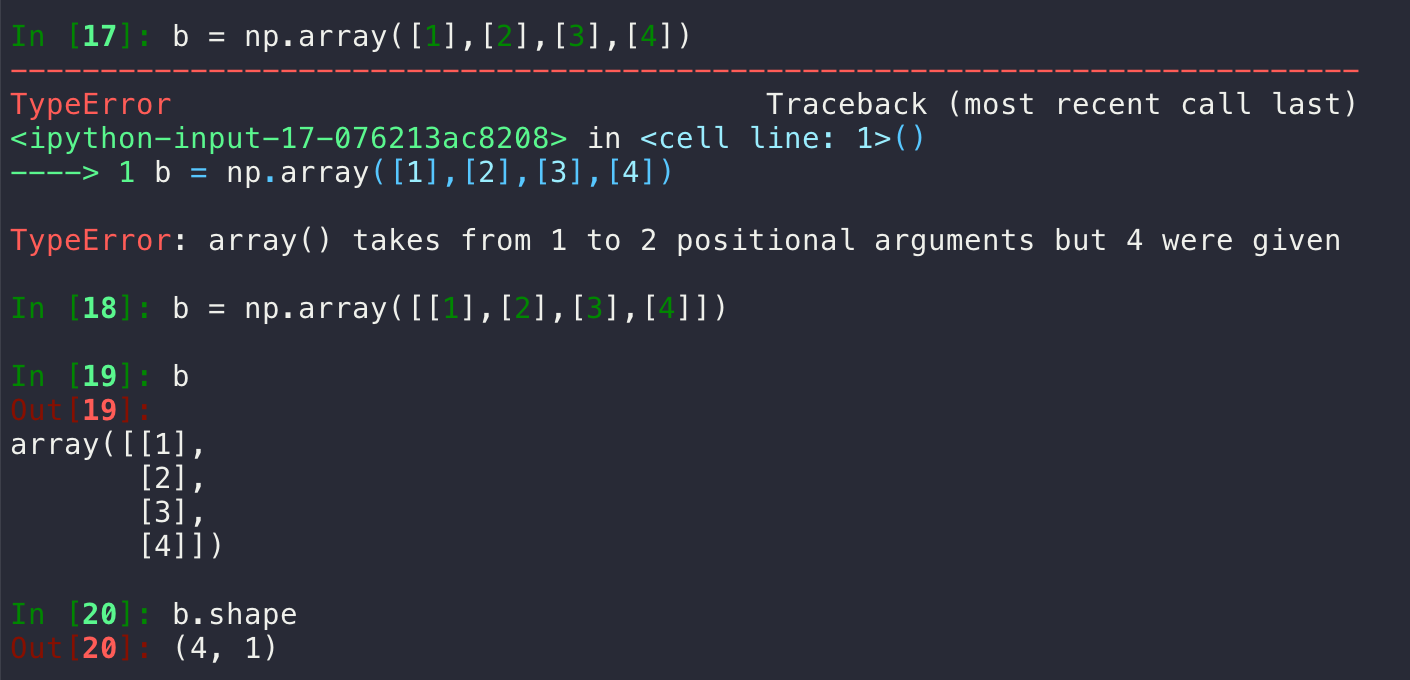
然后是从 b 到 a 的转换：

然后是从 b 到 b 的转换：

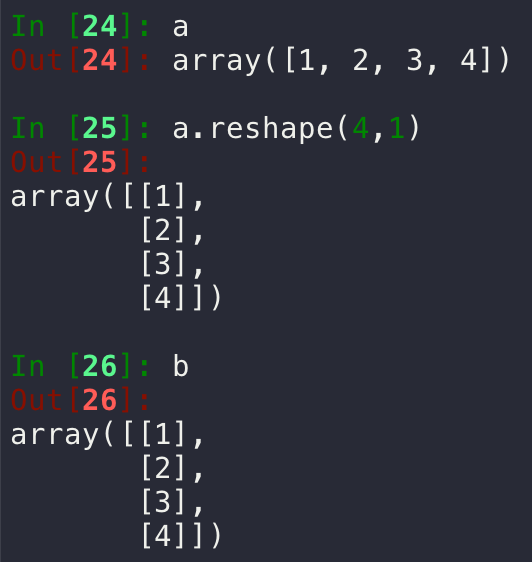
以及一段2021-11-02写的小程序：

import numpy as np

a = np.arange(8)  # a.shape为(8, -1)
print(a)
# [0 1 2 3 4 5 6 7]
print('\n')

print(a.reshape(8, 1))  # reshape以后有8行、1列，所以shape为(8, 1)
# [[0]
#  [1]
#  [2]
#  [3]
#  [4]
#  [5]
#  [6]
#  [7]]
print('\n')

print(a.reshape(8, -1))  # reshape以后有8行，但不指定有多少列，所以shape为(8, 1)
# [[0]
#  [1]
#  [2]
#  [3]
#  [4]
#  [5]
#  [6]
#  [7]]
print('\n')

# print(a.reshape(7, -1))  # reshape以后有7行，但不指定有多少列，所以会报错
# print('\n')

print(a.reshape(1, 8))  # reshape以后有1行、8列，所以shape为(1, 8)
# [[0 1 2 3 4 5 6 7]]
print('\n')

print(a.reshape(2, 4))  # reshape以后有2行、4列，所以shape为(2, 4)
# [[0 1 2 3]
#  [4 5 6 7]]
print('\n')

print(a.reshape(2, 4).reshape(-1))  # 一个2行、4列的数组/矩阵被降维成了1维vector，变回了(8, -1)
# [0 1 2 3 4 5 6 7]
print('\n')

Numpy数组操作(reshape, concatenate, vstack 等)

*后续补充内容：🔗 [2022-02-16 - Truxton's blog] https://truxton2blog.com/2022-02-16/

首先是一个最简单的：如何用numpy的版本实现“数组的拼接”，比如a=[1,2,3], b=[4,5,6]，现在要把a和b按a-b的顺序拼接起来的到[1,2,3,4,5,6]：

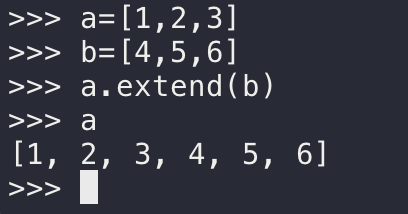
答案：使用 np.concatenate((a,b),axis=0) ：

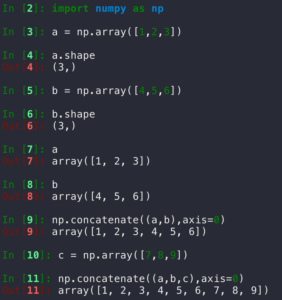
下面的内容主要参考：🔗 [Numpy 数组操作 | 菜鸟教程] https://www.runoob.com/numpy/numpy-array-manipulation.html

import numpy as np

a = np.arange(1, 9, 1).reshape(4, 2)
print('a:')
print(a)
print('\n')

b = np.arange(-1, -9, -1)
b = b.reshape(4, 2)
print('b:')
print(b)
print('\n')

print('np.vstack((a,b))')
print(np.vstack((a, b)))
print('\n')
print('np.concatenate((a,b),axis=0)')
print(np.concatenate((a, b), axis=0))
print('\n')
print('np.concatenate((a,b),axis=1)')
print(np.concatenate((a, b), axis=1))

结果：

a:
[[1 2]
 [3 4]
 [5 6]
 [7 8]]


b:
[[-1 -2]
 [-3 -4]
 [-5 -6]
 [-7 -8]]


np.vstack((a,b))
[[ 1  2]
 [ 3  4]
 [ 5  6]
 [ 7  8]
 [-1 -2]
 [-3 -4]
 [-5 -6]
 [-7 -8]]


np.concatenate((a,b),axis=0)
[[ 1  2]
 [ 3  4]
 [ 5  6]
 [ 7  8]
 [-1 -2]
 [-3 -4]
 [-5 -6]
 [-7 -8]]


np.concatenate((a,b),axis=1)
[[ 1  2 -1 -2]
 [ 3  4 -3 -4]
 [ 5  6 -5 -6]
 [ 7  8 -7 -8]]

import numpy as np

a = np.arange(1, 9, 1).reshape(8, )
print(a)
print('\n')
print(np.diag(a))

结果：

[1 2 3 4 5 6 7 8]


[[1 0 0 0 0 0 0 0]
 [0 2 0 0 0 0 0 0]
 [0 0 3 0 0 0 0 0]
 [0 0 0 4 0 0 0 0]
 [0 0 0 0 5 0 0 0]
 [0 0 0 0 0 6 0 0]
 [0 0 0 0 0 0 7 0]
 [0 0 0 0 0 0 0 8]]

import numpy as np

a = np.array([0.5, 0.4, 0.1, 0.6, 0.2, 0.9, 0.5])
a[np.where(a >= 0.5)] = 1
a[np.where(a < 0.5)] = 0
print(a)

结果：

[1. 0. 0. 1. 0. 1. 1.]

参考了：🔗 [python - Concatenating two one-dimensional NumPy arrays - Stack Overflow] https://stackoverflow.com/questions/9236926/concatenating-two-one-dimensional-numpy-arrays

import matplotlib.pyplot as plt
import numpy as np

a = np.linspace(1, 1, 30)
b = np.linspace(2, 2, 30)
c = np.linspace(3, 3, 30)
d = np.linspace(4, 4, 30)
e = np.linspace(5, 5, 30)
f = np.linspace(4, 4, 30)
g = np.linspace(3, 3, 30)
h = np.linspace(2, 2, 30)
i = np.linspace(1, 1, 30)

print('a: ' + str(a))
print('b: ' + str(b))
print('c: ' + str(c))

concat = np.concatenate([a, b, c, d, e, f, g, h, i])
plt.figure()
plt.scatter(x=np.linspace(1, 270, 270), y=concat)
plt.savefig('1.png')

结果：

a: [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1.]
b: [2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.
 2. 2. 2. 2. 2. 2.]
c: [3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3. 3.
 3. 3. 3. 3. 3. 3.]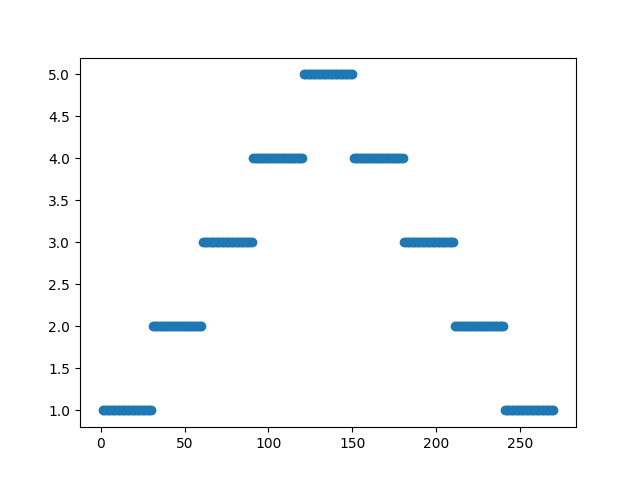

广义线性模型 GLM

🔗 [2021-10-20 - Truxton's blog] https://truxton2blog.com/2021-10-20/

此外还有：🔗 [广义线性模型（GLM）概述 - 知乎] https://zhuanlan.zhihu.com/p/420499972

回顾linear regression: 🔗 [Machine Learning 1: Linear Regression] https://cs.stanford.edu/~ermon/cs325/slides/ml_linear_reg.pdf

🔗 [(ML 10.1) Bayesian Linear Regression - YouTube] https://www.youtube.com/watch?v=1WvnpjljKXA

复习线性代数norm: 🔗 [CS412_19_Mar_2013.pdf] http://pages.cs.wisc.edu/~sifakis/courses/cs412-s13/lecture_notes/CS412_19_Mar_2013.pdf