WARNING: This article may be obsoleteThis post was published in 2021-10-01. Obviously, expired content is less useful to users if it has already pasted its expiration date.
This article is categorized as "Garbage" . It should NEVER be appeared in your search engine's results.主要内容：SVG, （单变量）随机变量的函数分布，uniform distribution, 均匀分布，Univariate，Bivariate random variable入门知识，边缘密度，二维正态分布，积分公式
SVG工具：
WordPress SVG plugin: https://wordpress.org/plugins/svg-support/
SVG拼接（cli），类似于 $ convert +append ：https://github.com/astraw/svg_stack
SVG压缩优化：https://github.com/svg/svgo
（单变量）随机变量的函数分布
一些基本性质：
[mathjax-d]\mathbb{P}[a<X \leq b]=F_{X}(b)-F_{X}(a)=\int_{a}^{b} f_{X}(x) d x[/mathjax-d] [mathjax-d]f(x) \geq 1[/mathjax-d] [mathjax-d]\int_{-\infty}^{\infty} f(x) \mathrm{d} x =1[/mathjax-d]例题：《浙大概率论》P51开始
例题：https://math.stackexchange.com/questions/3720710/pdf-of-y-x2-when-x-is-uniform-on-1-1
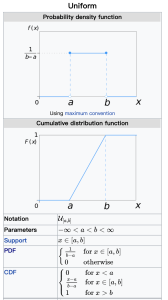
uniform distribution, 均匀分布
基本概念，来自https://en.wikipedia.org/wiki/Continuous_uniform_distribution
上面的图使用[mathjax]u_{[a,b]}[/mathjax]来表示均匀分布。或者：[mathjax]X\sim U(a,b)[/mathjax].
Univariate
Univariate is a term commonly used in statistics to describe a type of data which consists of observations on only a single characteristic or attribute. https://en.wikipedia.org/wiki/Univariate_(statistics)
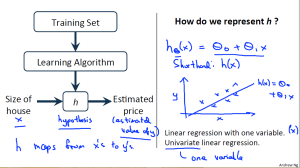
这可能是各类ML公开课linear regression中最常见的部分：
Univariate random variable and PDF（连续型随机变量及其密度函数）
📚 https://www.bilibili.com/video/BV1vW41147Uw?p=20
Bivariate random variable入门知识：
📚《浙大概率论》p60开始
⚠️连续型随机变量单点概率为0
二重积分的计算方法：https://zhuanlan.zhihu.com/p/38594716
例题：（见https://www.bilibili.com/video/BV1vW41147Uw?p=33），或者在《浙大概率论》p63也有类似的题目：
边缘密度：
设连续型随机变量[mathjax](X,Y)[/mathjax]的概率密度为[mathjax]f(x,y)[/mathjax]，则：
[mathjax-d]f_{X}(x)=\int_{-\infty}^{\infty} f(x, y) \mathrm{d} y[/mathjax-d] [mathjax-d]f_{Y}(y)=\int_{-\infty}^{\infty} f(x, y) \mathrm{d} x[/mathjax-d]以上[mathjax]f_{X}(x)[/mathjax]和[mathjax]f_{Y}(y)[/mathjax]分别是[mathjax](X,Y)[/mathjax]关于[mathjax]X[/mathjax]和关于[mathjax]Y[/mathjax]的边缘概率密度。
例题：《浙大概率论》p66
二维正态分布：
（详细证明见《浙大概率论》p66）
设二维随机变量[mathjax](X,Y)[/mathjax]的概率密度为：
[mathjax-d]\begin{aligned} f(x, y)=& \frac{1}{2 \pi \sigma_{1} \sigma_{2} \sqrt{1-\rho^{2}}} \exp \left\{\frac { - 1 } { 2 ( 1 - \rho ^ { 2 } ) } \left[\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}} -2 \rho \frac{\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1} \sigma_{2}}+\frac{\left(y-\mu_{2}\right)^{2}}{\sigma_{2}^{2}}\right]\right\} \end{aligned}[/mathjax-d]那么[mathjax](X,Y)[/mathjax]服从二维正态分布，边缘概率密度为：
[mathjax-d]f_{X}(x)=\frac{1}{\sqrt{2 \pi} \sigma_{1}} \mathrm{e}^{-\frac{\left(x-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}}, \quad-\infty<x<\infty[/mathjax-d] [mathjax-d]f_{Y}(y)=\frac{1}{\sqrt{2 \pi} \sigma_{2}} \mathrm{e}^{-\frac{\left(y-\mu_{1}\right)^{2}}{2 \sigma_{2}^{2}}}, \quad-\infty<y<\infty[/mathjax-d]积分公式：[mathjax-d]\int udv=uv-\int vdu[/mathjax-d] [mathjax-d]\frac{d}{d x}\left(\frac{f(x)}{g(x)}\right)=\frac{g(x) f^{\prime}(x)-f(x) g^{\prime}(x)}{(g(x))^{2}}[/mathjax-d]
